As a final project for my mathematical-physics class I explored the categorical equivalence between 2-dimensional topological quantum field theories (TQFT) and the category of commutative Frobenius algebras. This led to an interesting study paper, which I'm now making publicly accessible.

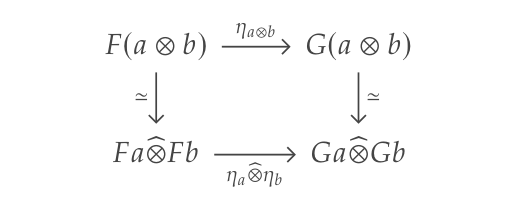
Monoidal natural transformation
Universal property of monoidal natural transformations

The paper is divided into 9 sections:

  1. Monoidal categories: This section serves as the foundation language of the paper, monoidal categories and their properties.
  2. Braided & symmetric monoidal categories: Here, we briefly delve into a special class of monoidal categories that permit commutative behaviour with respect to the associated bifunctor product.
  3. Cobordisms: Central idea to topological quantum field theories is the idea of gluing smooth compact manifolds without boundary, which is what cobordisms are all about.
  4. Elements of Morse theory: We provide a very introductory discussion of Morse theory, just showing some key results required for the rest of the paper.
  5. The category n-cob: One of the building blocks of the main theorem of the paper is the category of cobordisms of a given dimension n, comprised compact oriented (n - 1)-dimensional manifolds.
  6. Monoidal structure of n-cob: As expected, the category of cobordisms exhibits some good properties, and in particular it admits a monoidal structure.
  7. Frobenius Algebras: Within the framework of monoidal categories, we study our second main character of our study in the paper, Frobenius algebras.
  8. Topological quantum field theories: In this section we can finally define what we mean by a TQFT.
  9. Equivalence theorems: Reaching to the climax of the paper, we delve into the theorems that motivated the paper's creation in the first place.

You can access the paper here.